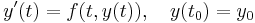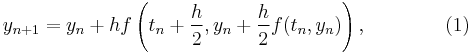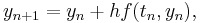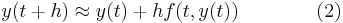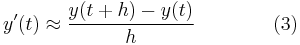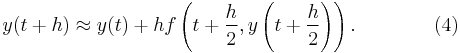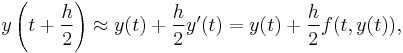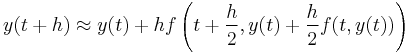Midpoint method

For the midpoint rule in numerical quadrature, see rectangle method.

In numerical analysis, a branch of applied mathematics, the midpoint method is a one-step method for solving the differential equation

$y'(t) = f(t, y(t)), \quad y(t_0) = y_0$

numerically, and is given by the formula

$y_{n%2B1} = y_n %2B hf\left(t_n%2B\frac{h}{2},y_n%2B\frac{h}{2}f(t_n, y_n)\right), \qquad\qquad (1)$

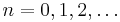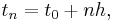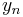for $n=0, 1, 2, \dots$ Here, $h$ is the step size — a small positive number, $t_n=t_0 %2B n h,$ and $y_n$ is the computed approximate value of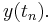 $y(t_n).$

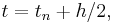The name of the method comes from the fact that in the formula above the function $f$ is evaluated at $t=t_n%2Bh/2,$ which is the midpoint between 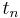$t_n$ at which the value of y(t) is known and 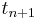$t_{n%2B1}$ at which the value of y(t) needs to be found.

The local error at each step of the midpoint method is of order 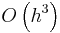$O\left(h^3\right)$ , giving a global error of order 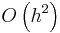$O\left(h^2\right)$ . Thus, while more computationally intensive than Euler's method, the midpoint method generally gives more accurate results.

The method is an example of a class of higher-order methods known as Runge-Kutta methods.

Derivation of the midpoint method

The midpoint method is a refinement of the Euler's method

$y_{n%2B1} = y_n %2B hf(t_n,y_n),\,$

and is derived in a similar manner. The key to deriving Euler's method is the approximate equality

$y(t%2Bh) \approx y(t) %2B hf(t,y(t)) \qquad\qquad (2)$

which is obtained from the slope formula

$y'(t) \approx \frac{y(t%2Bh) - y(t)}{h} \qquad\qquad (3)$

and keeping in mind that 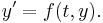$y' = f(t, y).$

For the midpoint method, one replaces (3) with the more accurate

$y'\left(t%2B\frac{h}{2}\right) \approx \frac{y(t%2Bh) - y(t)}{h}$

when instead of (2) we find

$y(t%2Bh) \approx y(t) %2B hf\left(t%2B\frac{h}{2},y\left(t%2B\frac{h}{2}\right)\right). \qquad\qquad (4)$

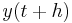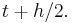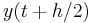One cannot use this equation to find $y(t%2Bh)$ as one does not know $y$ at $t%2Bh/2.$ The solution is then to use a Taylor series expansion exactly as if using the Euler method to solve for $y(t%2Bh/2)$ :

$y\left(t %2B \frac{h}{2}\right) \approx y(t) %2B \frac{h}{2}y'(t)=y(t) %2B \frac{h}{2}f(t, y(t)),$

which, when plugged in (4), gives us

$y(t %2B h) \approx y(t) %2B hf\left(t %2B \frac{h}{2}, y(t) %2B \frac{h}{2}f(t, y(t))\right)$

and the midpoint method (1).

References

Griffiths,D. V.; Smith, I. M. (1991). Numerical methods for engineers: a programming approach. Boca Raton: CRC Press. p. 218. ISBN 0-8493-8610-1.

Numerical integration

First order methods	Euler method · Backward Euler · Semi-implicit Euler · Exponential Euler

Second order methods	Verlet integration · Velocity Verlet · Crank–Nicolson method · Beeman's algorithm · Midpoint method · Heun's method · Newmark-beta method · Leapfrog integration

Higher order methods	Runge–Kutta methods · List of Runge–Kutta methods · Linear multistep method

Midpoint method

Derivation of the midpoint method

See also

References